


На главную страницу | Новости | FAQ | Ссылки | Для детей | Контакты
Их результатом было открытие двух типов клеток, влияющих на зрительную восприимчивость: первые обладают свойством локальной чувствительности и предназначены для выделения элементарных характеристик образов (ориентированных краев, конечных точек, углов), вторые же путем их комбинирования осуществляют построение высокоуровневых признаков.
Известны различные реализации сверточных нейронных сетей, отличающиеся топологией слоев, способом организации процесса обучения и другими признаками.
Исходя из результатов их применения в решении задач классификации, аналогичных рассматриваемой, и возможностей обучения сети без использования специализированного аппаратного обеспечения, в качестве базовой для проведения исследовательской работы была выбрана нейросетевая модель
В ее основе лежат три
1) локальные рецептивные поля (нейроны получают входной сигнал от окрестностей нейронов предыдущего слоя, за счет чего сеть обучается двумерной структуре входного образа);
2) разделяемые веса (нейроны слоя объединены картами, в которых они обладают общими весами, при этом карты генерируют различные признаки и сокращают количество параметров, настраиваемых в ходе обучения);
3) пространственные подвыборки (локальное усреднение откликов карт приводит к синтезу высокоуровневых признаков и повышает инвариантность сети к искажениям) [3, 4].
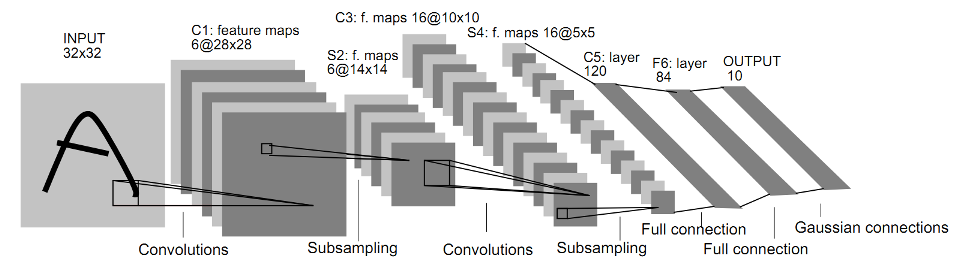
Пример структуры сверточной нейронной сети представлен на Рисунке. Сверточная сеть состоит из слоев разных типов, которые будут описаны далее по тексту.
Операция свертки изображения - это операция между матрицей изображения и матрицей-ядром (фильтром), при которой каждый элемент (пиксель) в выходном изображении есть сумма произведений значения элемента ядра на значение соответствующего покрываемого элемента матрицы входящего изображения [5]. Математически операция свертки записывается следующим образом:
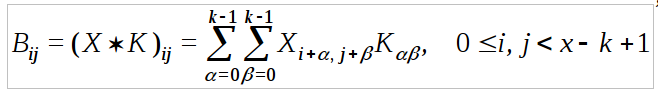
где X - матрица размера x на x, задающая входное изображение; K - матрица размера k на k, которая называется ядром свертки; B - результат свертки матрицы X с ядром K. Наглядно оперция свертки показана на рисунке:
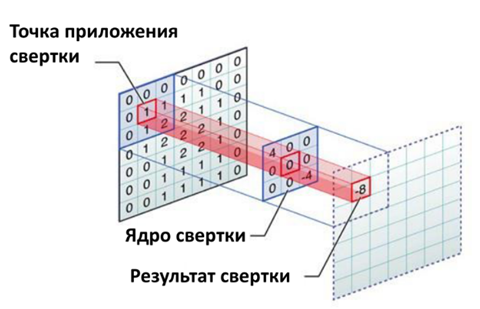
В свёрточной нейронной сети в операции свёртки используется лишь ограниченная матрица весов небольшого размера, которую «двигают» по всему обрабатываемому слою (в самом начале --непосредственно по входному изображению), формируя после каждого сдвига сигнал активации для нейрона следующего слоя с аналогичной позицией.
Для различных нейронов выходного слоя используются одна и та же матрица весов, которая представляет собой ядро свёртки. Её интерпретируют как графическое кодирование какого-либо признака, например, наличие наклонной линии под определенным углом. Тогда следующий слой, получившийся в результате операции свёртки такой матрицей весов, показывает наличие данного признака в обрабатываемом слое и её координаты, формируя так называемую карту признаков. А именно если в результате применения фильтра на данную область входного изображения получается достаточно большое число, то это означает, что был найден искомый признак. Если же получается маленькое число, то признак не распознан.
Таким образом, операция свертки используется в СНС для составления карт признаков. В свёрточной нейронной сети присутствует целая гамма таких фильтров, кодирующих элементы изображения (например линии и дуги под разными углами).
Заметим, что ядра свертки не закладываются пользователем заранее, а формируются самостоятельно путём обучения сети, например классическим методом распространения ошибки.
Проход каждым набором весов формирует свой собственный экземпляр карты признаков, делая нейронную сеть многоканальной, т.е. с несколькими независимыми картами признаков в пределах одного сверточного слоя.
Также, следует отметить, что при прохождении фильтром изображения, фильтр передвигают обычно не на полный шаг (размер матрицы весов фильтра), а на небольшое расстояние. Так, например, при размерности матрицы весов 5 на 5, соответствующий фильтр каждый раз перемещается только на один или два пикселя вместо пяти, чтобы не «перешагнуть» искомый признак.
Особенностью свёрточного слоя является сравнительно небольшое количество параметров, устанавливаемое при обучении.
Так например, пусть исходное изображение имеет размерность 100 на 100 пикселей и поступает по трём каналам, а свёрточный слой использует фильтры c ядром 3 на 3 пикселя с выходом на 6 каналов. Для каждого фильтра с таким ядром количество настраиваемых параметров равно количеству элементов в ядре (матрице весов) - 9 параметров.
Тогда общее количество настраиваемых параметров, учитывая сочетания всех каналов, будет равно 3*6*9 =152, что существенно меньше количества искомых параметров в случае, если бы для той же задачи использовалась полносвязная нейронная сеть.
База данных рукописных цифр MNIST - общепризнанный эталон, на котором часто тестируется качество алгоритмов распознавания изображений. Для распознавания рукописных цифр предложено несколько разных структур сверточных сетей, для которых максимальная точность распознавания на тестовой выборке составила 99,14% - 99,39%. Например, в работе [
В настоящей работе эти показатели будут улучшены за счет увеличения количества карт признаков в сверточных слоях, использования двух скрытых полносвязных слоев и применения техники временного «выбрасывания» (dropout) нейронов из полносвязных слоев в процессе обучения. Кроме того, будет проведено сравнение эффективности распознавания изображений рукописных цифр с помощью сверточных и полносвязных нейронных сетей, изучено влияние размера ядра свертки и количества карт признаков в сверточных слоях на точность распознавания и время обучения сетей.
Существует еще несколько простых приемов, позволяющих повысить точность распознавания сверточных сетей. Во-первых, это внесение небольших искажений в обучающую выборку при переходе на следующую эпоху, что по сути эквивалентно увеличению обучающей выборки и позволяет частично или полностью устранить проблему переобучения. Во-вторых, это использование совокупности сверточных сетей разной структуры, либо одной структуры с разными начальными весами (так называемые «комитеты СНН») [
Основной критерий эффективности алгоритма распознавания - это, конечно, точность классификации. Однако на практике важно также время работы алгоритма, а именно время обучения (настройки весов), которое в случае глубоких многослойных нейросетей может оказаться слишком большим и неприемлемым для практических приложений. Благодаря меньшему количеству связей сверточные сети обучаются быстрее по сравнению с полносвязными сетями с тем же количеством слоев, однако даже для сверточных сетей время обучения может составлять несколько часов или дней в зависимости от ее глубины (количество слоев) и ширины (количество карт признаков). Поэтому часто приходится искать компромисс между точностью распознавания и временем обучения.
Для программной реализации нейросетевых алгоритмов использовалась библиотека Theano языка Python. Эта библиотека содержит необходимый набор математических функций для работы c многомерными массивами (тензорами). Кроме того, эта библиотека позволяет задействовать в ходе вычислений графический процессор (при включенной поддержке технологии CUDA), что в несколько раз повышает скорость обучения нейронной сети по сравнению с использование только центрального процессора. Операция двумерной свертки реализуется с помощью метода theano.tensor.signal.conv2d(), а операция "макс-пулинга" - с помощью theano.tensor.signal.pool.pool_2d(). В качестве аппаратной части использовался процессор Intel Core 2 6320@1,86 ГГц и графическая карта GeForce GT 610.
Обучение нейронных сетей осуществлялось по алгоритму обратного распространения ошибки, используя мини-пакетный градиентный спуск с заданным коэффициентом скорости ?, то есть модификация весов осуществлялась после обработки пакета из нескольких изображений обучаемой выборки. Длина пакета бралась равной 10.
Во избежание нежелательного переобучения сети на каждой итерации использовалась процедура временного «выбрасывания» (dropout) случайным образом 50% нейронов из скрытых полносвязных слоев (см.
Изучение точности распознавания и времени обучения проводилось для трех классов нейронных сетей:
1) сети, состоящие только из полносвязных слоев;
2) сверточные сети, не содержащие полносвязных слоев (не считая выходного softmax-слоя);
3) сети, включающие как сверточные, так и скрытые полносвязные слои.
Тестирование сетей проводилось на примере распознавания рукописных цифр базы MNIST. Эта база содержит изображения рукописных цифр в оттенках серого размером 28 на 28 пикселей (пример изображения показан на рис. 1). Обучающая выборка содержит 50000 изображений цифр, тестирующая выборка - 10000 изображений.
В таблице приведены результаты классификации рукописных цифр полносвязными и сверточными сетями после 40 эпох обучения с коэффициентом скорости обучения ? = 0,05. Одна эпоха соответствует одному прогону через сеть всей обучающей выборки базы MNIST.
# Структура нейронной сети | Время обучения, мин./эпоха | Ошибка распознавания %
1. 1@28x28 – S10 0,08 7,92
2. 1@28x28 – F200 – S10 0,16 1,87
3. 1@28x28 – F1000 – S10 0,54 1,57
4. 1@28x28 – F2000 – S10 1,10 1,51
5. 1@28x28 – (F1000)2 – S10 1,46 1,84
6. 1@28x28 – (F1000)3 – S10 2,34 2,07
7. 1@28x28 – 60@24x24/12x12 – S10 4,45 1,31
8. 1@28x28 – 15@24x24/12x12 – 60@8x8/4x4 – S10 7,24 0,94
9. 1@28x28 – 6@24x24/12x12 – 12@8x8/4x4 – 60@2x2/1x1 – S10 1,08 2,72
10. 1@28x28 – 15@24x24/12x12 – 60@8x8/4x4 – F200 – S10 7,64 0,54
11. 1@28x28 – 15@24x24/12x12 – 60@8x8/4x4 – F1000 – F200 – S10 (СНН-15-60) 8,41 0,48
12. 1@28x28 – 15@24x24/12x12 – 60@8x8/4x4 – (F1000)2 – F200 – S10 9,31 0,51
13. 1@28x28 – 15@26x26/13x13 – 60@8x8/4x4 – F1000 – F200 – S10 10,60 0,55
14. 1@28x28 – 15@22x22/11x11 – 60@8x8/4x4 – F1000 – F200 – S10 6,35 0,52
15. 1@28x28 – 15@20x20/11x11 – 60@6x6/3x3 – F1000 – F200 – S10 5,88 0,62
Рассмотрим вначале нейронные сети, состоящие только из полносвязных слоев, а именно сети вида 1@28x28 - (F1000)L - S10, где L – количество скрытых слоев, каждый из которых включает по 1000 нейронов. Как видно, лучший результат по точности распознавания дает двухслойная сеть №3 (с одним скрытым слоем). Увеличение количества скрытых слоев ухудшает результат. Это связано в первую очередь с тем, что при большом количестве слоев требуется больше итераций для минимизации функции стоимости. Увеличение количества нейронов в сети с одним скрытым слоем до 2000 дает увеличение точности на 0,06%, однако дальнейшее увеличение плотности не дало повышения точности. Таким образом, наилучшая точность распознавания рукописных цифры базы MNIST с помощью классических полносвязных сетей, обучаемых методом обратного распространения ошибки, составила 98,49% (ошибка 1,51%).
Далее рассмотрим три нейронных сети под номерами 7–9, в которых все скрытые слои являются сверточными либо слоями предвыборки. Во всех трех сетях последний сверточный слой содержит 60 карт признаков. Лучший результат 0,94% получен для сети №8 с двумя сверточными слоями.
В последующих строках таблицы представлены результаты для сверточных сетей, включающих два сверточных слоя и несколько скрытых полносвязных слоев. Оптимальное количество нейронов в полносвязных слоях было подобрано методом проб и ошибок. В обоих сверточных слоях использовалось ядро свертки размером 5x5. При входном размере изображения 28x28 такой размер фильтра является оптимальным. Это видно из сравнения сетей под номерами 11 и 13–15. В сети №13 использовались ядра свертки размером 3x3 и 6x6 в первом и втором сверточных слоях соответственно, в сети №14 – 7x7 и 4x4, в сети №15 – 9x9 и 5x5. Лучший результат (0,52%) получен для сети №14, однако он всё равно уступает сети №11 с ядрами 5x5 и 5x5.
Из сравнения точности распознавания для сетей под номерами 8 и 10 – 12 видно, что добавление по крайней мере одного скрытого полносвязного слоя в сверточную сеть позволяет уменьшить ошибку примерно в два раза. Сверточные сети с полносвязными скрытыми слоями показывают примерно одинаковый результат (ошибка в пределах 0,5 – 0,6%). Тем не менее, наименьшая ошибка распознавания 0,48% получена в случае двух скрытых полносвязных слоев, т.е. для сети вида CHH?f1?f2 (см. рис. 1). Поэтому далее проанализируем сверточные сети именно такой структуры.
На рис. 2 показаны зависимости ошибки распознавания и времени обучения сетей вида CHH?f1?60 и CHH?15?f2 от количества карт признаков в первом и втором скрытых слоях соответственно (с шагом в 5 карт признаков). Как видно, время обучения растет с увеличением количества карт признаков как в первом, так и во втором слое, и эта зависимость близка к линейной. Точность распознавания сначала улучшается с увеличением количества карт признаков, однако в некоторый момент наступает насыщение и дальнейшее добавление карт признаков не дает заметного улучшения. Так, для класса сетей CHH-f1-60 оптимальное значение количества карт признаков в первом слое составляет 15 – 20, дальнейшее же увеличение не приводит к уменьшению ошибки распознавания. Среди сетей вида CHH-15-f2 лучший результат по отношению ошибки распознавания ко времени обучения показывает сеть с f2 = 15, для которой ошибка составила 0,51%, а общее время обучения 160,8 минут. В случае же, если точность распознавания критична, то необходимо использовать сети с количеством карт признаков 55 – 60, для которых ошибка составила 0,48%, однако время обучения таких сетей будет в два раза больше (310,4 – 330,0 минут).
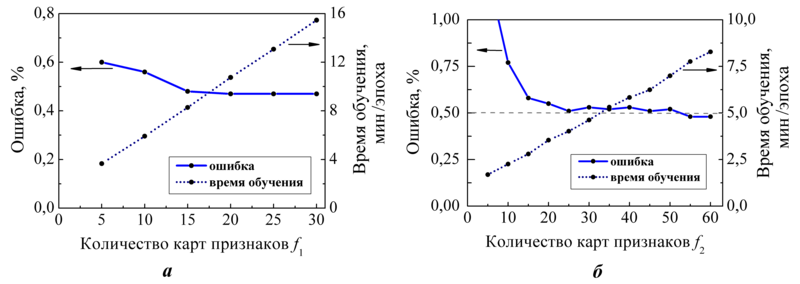
*Рис. 2. Влияние количества карт признаков (f1, f2) в сверточных слоях сетей вида CHH-f1-f2 на ошибку распознавания и время обучения: а – зависимость от f1 при f2 = 60; б – зависимость от f2 при f1 = 15.
Отметим, что одинаковая продолжительность обучения в 40 эпох для всех рассмотренных нейронных сетей была выбрана для удобства их тестирования. Однако полученная точность распознавания на этом этапе не являются максимально достижимой. Дальнейшее повышение точности возможно за счет дообучения сети с меньшим значением коэффициента скорости обучения ?. На рис. 3 показан график изменения ошибки распознавания по эпохам для двух сверточных сетей: на первых 40 эпохах использовалось значение ? = 0,05, на последующих 40 эпохах ? = 0,02. Малое значение ? делает график обучения более плавным и позволяет повысить точность распознавания. Для сети СНН-15-15 на дополнительных 40 эпохах ошибка была понижена с 0,60% до 0,52%; для сети CHH-15-60 – с 0,48% до 0,42%.
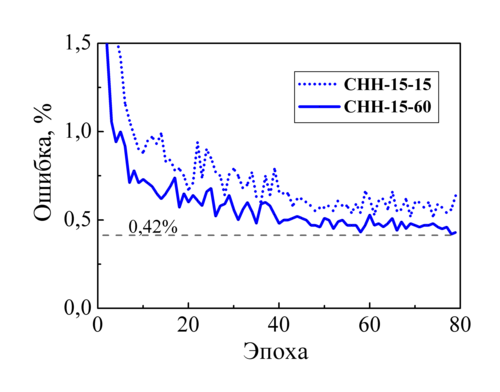
*Рис. 3. Изменение ошибки распознавания в процессе обучения сверточных нейронных сетей CHH-15-15 и CHH-15-60.
Сверточные нейронные сети показывают хорошие результаты в задаче распознавания рукописных цифр по сравнению с классическими полносвязными сетями прямого распространения. Однако для качественного распознавания изображений также требуется наличие в сверточной сети скрытых полносвязных слоев. Нейронная сеть CHH-15-60, состоящая из двух сверточных слоев из 15 и 60 карт признаков, двух слоев макс-пулинга, двух скрытых полносвязных слоев и выходного softmax-слоя, позволяет достичь ошибки распознавания 0,48% за 40 эпох обучения, причем этот результат может быть улучшен до 0,42% за счет дообучения такой сети с коэффициентом скорости обучения ? = 0,02.
Оптимальное количество карт признаков зависит от сложности распознаваемых образов. Для относительно несложных образов, таких как десятичные цифры, достаточно использовать порядка 15 карт признаков в первом сверточном слое и 25 во втором. Дальнейшее увеличение количества карт признаков не приводит к ощутимому повышению точности распознавания, однако заметно увеличивает время обучения сети.
1. Hubel, D.H. Receptive fields, binocular interaction and functional architecture in the cat's visual cortex / D.H. Hubel, T.N. Wiesel // Journal of Physiology London. - 1962. - Vol. 15. - P. 106-154.
2. LeCun, Y. Gradient-based learning applied to document recognition / Y. LeCun [et al.] // Proc. of the IEEE. - 1998. - Vol. 86. - P. 1-46.
3. Кузьмицкий, Н.Н. Сверточная нейросетевая модель в задача классификации цифр / Н.Н. Кузьмицкий // Доклады БГУИР. - 2012. - N7. - С. 64-70.
4. Хайкин, С. Нейронные сети: полный курс / С. Хайкин. - 2-е изд. : Пер. с англ. - М.: ООО "И.Д.Вильямс", 2016. - 1104 с.
5. Красильников, Н. Н. Цифровая обработка 2D- и 3D-изображений: учеб. пособие / Н.Н.Красильников. - М.: ООО «БХВ-Петербург», 2011. - 602 с.
6. Самое главное о нейронных сетях. Лекция в Яндексе:
https://habrahabr.ru/company/yandex/blog/307260/
7. Rectified Linear Units Improve Restricted Boltzmann Machines:
http://machinelearning.wustl.edu/mlpapers/paper_files/icml2010_NairH10.pdf
8. Что такое сверточная нейронная сеть
https://habrahabr.ru/post/309508/
9. Кухарев А.В., Махлаев Ю.Н. Нейронные сети на основе операции свертки для эффективного распознавания рукописных цифр // Вестник ВГУ, 2017.
https://vsu.by/vesnik-vdu/poslednij-vypusk.html





Now 15.07.25 23:44:57, Your IP: 216.73.216.237; arduino.zl3p.com/robots/NN_CNN
ePN